Question

What is the inverse of the function f(x) = 2x + 1?

1. h(x) = one-halfx – one-half

2. h(x) = one-halfx + one-half

3. h(x) = one-halfx – 2

4. h(x) = one-halfx + 2

Answer 1

Answer: OPTION 1

Explanation:

Given the function f(x):

`f(x) = 2x + 1`

You can follow these steps in order to find its inverse function h(x):

- Rewrite it with
`f(x)=y`:

`y= 2x + 1`

- Solve for "x":

`y-1=2x\\\\(y-1)/(2)=x\\\\ x=(1)/(2)y-(1)/(2)`

- Exchange the variables:

`y=(1)/(2)x-(1)/(2)`

- Rewrite it with
`y=h(x)`. Then:

`h(x)=(1)/(2)x-(1)/(2)`

Answer 2

`f^(-1)(x)=(1)/(2)x-(1)/(2)` ⇒ answer 1

Explanation:

* Lets explain how to find the inverse of a function

- To find the inverse of a function :

# Write y = f(x)

# Switch the x and y

# Solve to find the new y

# The new y is
`f^(-1)`

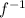
* Lets solve the problem

∵ f(x) = 2x + 1

- Put y = f(x)

∴ y = 2x + 1

- Switch x and y

∴ x = 2y + 1

- Solve to find the new y

∵ x = 2y + 1

- Subtract 1 from both sides

∴ x - 1 = 2y

- Divide both sides by 2

∴ (x - 1)/2 = y

- Divide each term in the left hand side by 2

∴ y = 1/2 x - 1/2

- Replace y by
`f^(-1)`

∴
`f^(-1)(x)=(1)/(2)x-(1)/(2)`

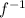
* The inverse of the function is
`f^(-1)(x)=(1)/(2)x-(1)/(2)`