Question

Concentrated hydrogen peroxide solutions are explosively decomposed by traces of transition metal ions (such as Mn or Fe): 2H2O2(aq) ---> 2H2O(l) + O2(g)

What volume of pure O2(g), collected at 27C and 746 torr, would be generated by decomposition of 125 g of a 50.0% by mass hydrogen peroxide solution?

Answer 1

23.0733 L

Step-by-step explanation:

The mass of hydrogen peroxide present in 125 g of 50% of hydrogen peroxide solution:

`Mass=\frac {50}{100}* 125\ g`

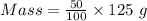
Mass = 62.5 g

Molar mass of
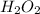`H_2O_2` = 34 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

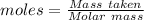
Thus, moles are:

`moles= (62.5\ g)/(34\ g/mol)`

`moles= 1.8382\ mol`

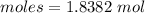
Consider the given reaction as:

`2H_2O_2_((aq))\rightarrow2H_2O_((l))+O_2_((g))`

2 moles of hydrogen peroxide decomposes to give 1 mole of oxygen gas.

Also,

1 mole of hydrogen peroxide decomposes to give 1/2 mole of oxygen gas.

So,

1.8382 moles of hydrogen peroxide decomposes to give
`\frac {1}{2}* 1.8382 mole of oxygen gas. </p><p>Moles of oxygen gas produced = 0.9191 mol</p><p>Given: </p><p>Pressure = 746 torr </p><p>The conversion of P(torr) to P(atm) is shown below: </p><p>[tex]P(torr)=\frac {1}{760}* P(atm)`

So,

Pressure = 746 / 760 atm = 0.9816 atm

Temperature = 27 °C

The conversion of T( °C) to T(K) is shown below:

T(K) = T( °C) + 273.15

So,

T₁ = (27 + 273.15) K = 300.15 K

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.0821 L.atm/K.mol

Applying the equation as:

0.9816 atm × V = 0.9191 mol × 0.0821 L.atm/K.mol × 300.15 K

⇒V = 23.0733 L