Answer:
The required length is 20 feet.
Explanation:
Let the length be = L
Let the width be = W
The length of a rectangular floor is twice its width.
This becomes:
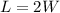
The length of the carpet is L
As given the carpet width is 2 feet less than the room, so
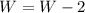
Area of the carpet is given as = 160 square feet
So, Area becomes:
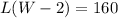
As L=2W, we get;
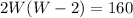
=>
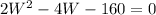
Taking out 2 common, we get;
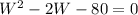
Solving this quadratic equation, we get:
(W-10) and (W+8)
Hence, W = 10 and W = -8(neglect this negative value)
Now, the width = 10 feet
And Length =
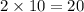 feet
feet
So, the required length is 20 feet.