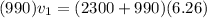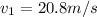Answer:
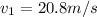
Step-by-step explanation:
Since we know that coefficient of the friction on the road is given as
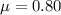
here the distance that the two cars will move is given as
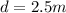
now we can find the speed just after two cars are locked together

here we know that acceleration is due to friction

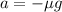
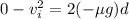
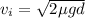
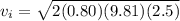

now by momentum conservation of two cars

so we have