Answer:
The measure of arc ADB is 292°.
Explanation:
Given information: Arc(AB)=68°
Points A and B lie on circle C, and point D lies on the major arc formed by A and B.
It means point A and D divides the circle C in two parts.
Arc(AB) = Minor arc by A and B.
Arc(ADB) = Major arc by A and B.
If two points lie on a circle, then

In circle C,
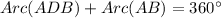
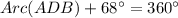
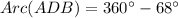

Therefore the measure of arc ADB is 292°.