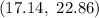Question

The class sizes of elementary school classes in a public school district are normally distributed with an unknown population mean and standard deviation. A random sample of 27 classes is taken and results in a sample mean of 20 students and sample standard deviation of 6 students. The margin of error for a 98% confidence interval estimate for the population mean using the Student's t-distribution is 2.86. Find a 98% confidence interval estimate for the population mean using the Student's t-distribution.

Answer 1

Answer:
`(17.14,\ 22.86)`

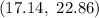
Explanation:

The confidence interval estimate for the population mean is given by :-

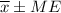`\overline{x}\pm ME`, where
`\overline{x}` is the sample mean and ME is the margin of error.

Given : Sample mean:
`\overline{x}=20`

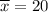
The margin of error for a 98% confidence interval estimate for the population mean using the Student's t-distribution :
`ME=2.86`

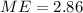
Now, the confidence interval estimate for the population mean will be :-

`20\pm2.86=(20-2.86,\ 20+2.86)=(17.14,\ 22.86)`

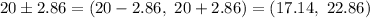
Hence, the 98% confidence interval estimate for the population mean using the Student's t-distribution =
`(17.14,\ 22.86)`