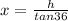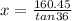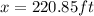Question

A man is flying in a hot-air balloon in a straight line at a constant rate of 5 feet per second, while keeping it at a constant altitude. As he approaches the parking lot of a market, he notices that the angle of depressions from his balloon to a friend's car in the parking lot is 35 ∘ . A minute and a half later, after flying directly over this friend's car, he looks back to see if friend getting into the car and observes the angle of depression to be 36 ∘ . At that time, what is the distance between him and his friend? (Round to the nearest foot.)

Answer 1

`x = 220.85 ft`

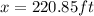
Step-by-step explanation:

Let at any moment of time the friend's car is at some horizontal distance "x" from the position of balloon.

Now if the altitude of the balloon is fixed and it is at height "h"

so here we will have

`tan \theta = (h)/(x)`

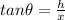
now we know that

initially the angle of the friend's car is 35 degree

so the horizontal distance will be

`x_1 = h cot35`

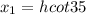
similarly if the angle after passing the car position is 36 degree

then we have

`x_2 = h cot36`

now the speed of the balloon is constant

so we have

`v = (x_1 + x_2)/(\Delta t)`

`5 ft/s = (h cot35 + h cot36)/(90 s)`

`5 ft/s = (2.8h)/(90)`

`h = 160.45 ft`

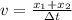
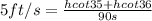
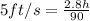
so the final position of friend when the angle is 36 degree

`x = (h)/(tan36)`

`x = (160.45)/(tan36)`

`x = 220.85 ft`