Question

The position of a particle moving on a straight line is given by s(t)=tan(4t). What is the acceleration of the particle at time t?

Answer 1

Acceleration of the particle is
`32tan(4t)sec^(2)(4t)`

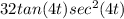
Step-by-step explanation:

Given that the position of the particle which is moving on the straight line is,

`s(t)=tan4(t)`

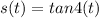
Differentiate it with respect to t will give the velocity,

`v=(ds)/(dt)\\ v=(d(tan4t))/(dt)\\ v=4sec^(2)(4t)`

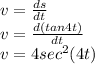
Now again differentiate it with respect to t to get acceleration.

`a=(dv)/(dt)\\ a=(d(4sec^(2)(4t) )/(dt) \\a=8sec(4t)(4)sec(4t)tan(4t)\\a=32tan(4t)sec^(2)(4t)`

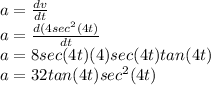
Therefore vthe acceleration of the particle is,
`32tan(4t)sec^(2)(4t).`