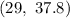Question

In a random sample of 30 people who rode a roller coaster one day, the mean wait time is 46.7 minutes with a standard deviation of 9.2 minutes. In a random sample of 50 people who rode a Ferris wheel the same day, the mean wait time is 13.3 minutes with a standard deviation of 1.9 minutes. Construct a 99% confidence interval for the difference between the mean wait times of everyone who rode both rides.

A. (31.7, 35.1)
B. (30.5, 36.3)
C. (29, 37.8)
D. (28.7, 38.1)

Answer 1

Answer: C.
`(29,\ 37.8)`

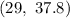
Explanation:

The confidence interval for difference of two population mean is given by :-

`\overline{x}_1-\overline{x}_2\pm z_(\alpha/2)\sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2)}`

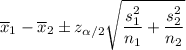
Given : Level of significance :
`1-\alpha:0.99`

Then , significance level :
`\alpha: 1-0.99=0.01`

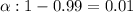
Critical value :
`z_(\alpha/2)=z_(0.005)=2.576`

`n_1=30\ ;\ n_2=50\\\\\overline{x}_1=46.7\ ;\ \overline{x}_2=13.3\\\\s_1=9.2\ ;\ s_2=1.9`

`46.7-13.3\pm(2.576)\sqrt{(9.2^2)/(30)+(1.9^2)/(50)}\approx33.4\pm4.38=(29.02\ ,37.78)\approx(29,\ 37.8)`

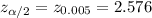
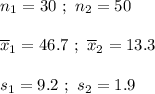
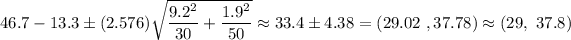
Hence, a 99% confidence interval for the difference between the mean wait times of everyone who rode both rides
`(29,\ 37.8)`