Answer with Step-by-step explanation:
We are given that
Length of flat piece of material =19 inches
Width of flat piece=4 inches
An open box is to be made from a flat piece by cutting equal squares of length x from the corners and folding up the sides
Therefore, length of open box=
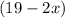 inches
inches
Width of open box=
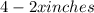
Height of box=
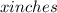
Volume of box=
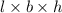
Substitute the values then we get
Volume of box=
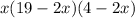
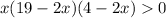
Because volume of open box is always greater than zero.
Then ,
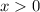
Substitute

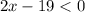
 By adding 19 on both sides
By adding 19 on both sides
Dividing by 2 on both sides
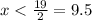
It means
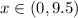
Substitute

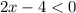
Adding 4 on both sides then we get
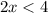
Dividing by 2 on both sides
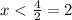

Then,
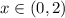
Therefore, domain of the box =
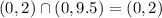
Then ,a=0 and b=2