Question:
A company produces boxes of DVDs at a rate of 52 boxes per hour they begin to produce boxes when they first opened for the day and after 3 hours have 400 boxes in stock.
- How many boxes were in stock when they opened?
- Write a linear model for the amount of boxes, b, as a function of the number of hours since they opened, h.
- Use your model to predict the number of boxes in stock at the end of an 8 hour shift.
Answer:
1.
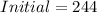
2.
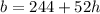
3. 660 boxes
Explanation:
Given
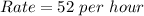
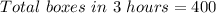
Solving (a): Initial Number of boxes
First, we calculate the number of boxes made in 3 hours
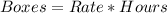
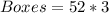
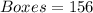
If they had 400 boxes at the 3rd hour.
Then, the number of boxes when they opened is:
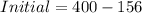
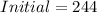
Solving (b): Linear function
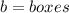
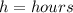
Since, we have the rate and the initial number of boxes.
The linear function is:
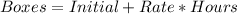
i.e.
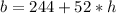
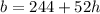
Solving (c): Boxes at the end of the 8th hour
We have:
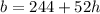
In this case:

Substitute 8 for h

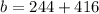

Hence, there are 660 boxes at the end of the 8th hour