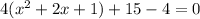Question

The equation 4x2 + 8x + 15 = 0 is being rewritten in vertex form.

Fill in the missing step.


Given 4x2 + 8x + 15 = 0
Step 1 4(x2 + 2x ___) + 15 ___ = 0
Step 2 ✔
Step 3 4(x + 1)2 + 11 = 0

A). 4(x2 + 2x + 1) + 15 − 4 = 0
B). 4(x2 + 2x + 1) + 15 − 1 = 0
C). 4(x2 + 2x + 2) + 15 − 2 = 0
D). 4(x2 + 2x + 4) + 15 − 4 = 0

Answer 1

A. 4(x^2 + 2x + 1) + 15 - 4 = 0

Explanation:

Because we have to make the expression in the brackets a perfect square by adding 1 and then, as we have introduce + 1 * 4 = + 4 into the equation, we must later subtract the 4.

Answer 2

(a)
`4(x^2+2x+1)+15-4=0`

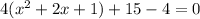
Explanation:

To solve this equation is necessary to remind the algebraic technique in which a quadratic function becomes a perfect square trinomial, i.e,
`ax^2+bx+c=0`.

Using this expression, it is possible to obtain a general criteria for completing any square trinomial regardless if the number is integer or real. To go further, it is necessary to rewrite the above expression as,

`a(x^2+(b)/(a)x)+c`

Likewise, it is convinient to remind the following rule; to complete a perfect square trinomial it is divided the first coefficient over the second term of the equation and then sum and subtract the square of the half of the second term, i.e,

`a(x^2+(b)/(a)x+((b)/(2a))^2-((b)/(2a))^2)+c=0`

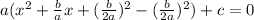
Using this generic expression, it is possible to solve the given problem in which the coefficients have these values a=4, b=8, c=15, hence

`4(x^2+(8)/(4)x+((8)/(2*4))^2-((8)/(2*4))^2)+15=0`,

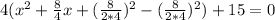Then,

`4(x^2+2x+1-1)+15=0`

Multiplying 4 with the bracket,

`4x^2+8x+4-4+15`

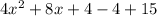
The question here is what to do with the +4 and -4. Right here is necessary to rewrite the expression as follows,

`(4x^2+8x+4)-4+15=0`

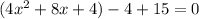
Then it uses the factorization of the common factor and the answer is obtained

`4(x^2+2x+1)+15-4=0`