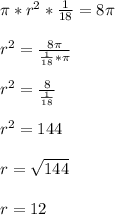Answer:
R= 12.
Explanation:
First of all, let's sketch up this case to better understand what's going on. Check the attatched image below.
1. Finding a relative value.
How much is 20° or the whole circle?
Remember that a circle makes a total angle of 360°, therefore, 20°/360° is the percentage that this area of 8pi represent for this circle.
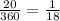 of the total circle.
of the total circle.
Therefore, if we multiply the area A by this value of
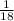 , we get the current value that we have, 8pi.
, we get the current value that we have, 8pi.
2. Constructing an equation.
Taking the information from step 1, the area of 8pi is given by the next expression:
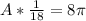
3. Rewrite the equation.
Remember that the formula for the area of a circle is the following:
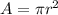
We can now substitute the equation of step 2 and write:
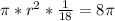
4. Solve the equation for r.