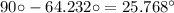Answer:
actual elevation angle above horizontal =
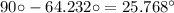
Given:
apparent angle =
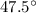
refractive index of water,
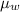 = 1.333
= 1.333
Solution:
angle of incidence,
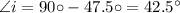
refractive index of water,
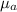 = 1
= 1
Using Snell's law:
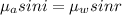
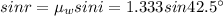
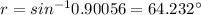
angle of refraction,
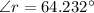
Now,
actual elevation angle above horizontal =