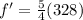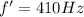Answer:
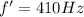
Step-by-step explanation:
Initially when fundamental frequency of the string is
f = 328 Hz
let the length of the string is Lo at this time
so we will have

now the length is shorten so that the frequency will change
final length is four fifth of the original length
so here we have

now we have

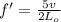
now we have
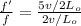
so we have
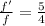
so the new fundamental frequency will be