Question

The points A(0, 0), B(0, 4a - 5) and C(2a + 1, 2a + 6) form a triangle. If angle ABC = 90, what is the area of triangle ABC?(A) 102(B) 120(C) 132(D) 144(E) 156

Answer 1

A:102

Explanation:

We are given that the points A(0,0),B(0,4a-5) and C(2a-+1,2a+6) form a triangle.

If angle ABC=
`90^(\circ)`

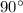
We have to find the area of triangle ABC

If angle ABC= 90 degree

From given below figure

`4a-5=2a+6`

`4a-2a=6+5`

`2a=11`

`a=(11)/(2)=5.5`

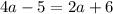
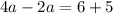
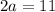
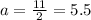
Substitute the values then we get

B(0,17) and C (12,17)

Distance formula

`√((x_2-x_1)^2+(y_2-y_1)^2)`

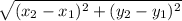
AB=
`√((0-0)^2+(17-0)^2)=17 units`

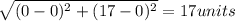
BC=
`√((12-0)^2+(17-17)^2)`

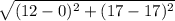
BC=
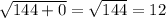`√(144+0)=√(144)=12` units

Area of triangle =
`(1)/(2)* b* h`

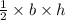
Substitute the values

Then we get

Area of triangle ABC=
`(1)/(2)* 17* 12`

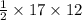
Area of triangle ABC=102 square units

Answer: A: 102