Question

A transect is an archaeological study area that is 1/5 mile wide and 1 mile long. A site in a transect is the location of a significant archaeological find. Let x represent the number of sites per transect. In a section of Chaco Canyon, a large number of transects showed that x has a population variance σ2 = 42.3. In a different section of Chaco Canyon, a random sample of 25 transects gave a sample variance s2 = 51.3 for the number of sites per transect. Use a 5% level of significance to test the claim that the variance in the new section is greater than 42.3. Find a 95% confidence interval for the population variance.

Answer 1

Answer:
`31.28\leq\sigma^2\leq99.29`

Explanation:

Confidence interval formula for population variance :-

`((n-1)s^2)/(\chi^2_(\alpha/2))\leq \sigma^2\leq((n-1)s^2)/(\chi^2_(1-\alpha/2))`

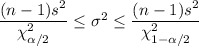
Given :
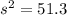`s^2 = 51.3` and
`n= 25`

Significance level :
`\alpha=0.05`

Using chi-square distribution, the Critical values are:

`\chi^2_(n-1, \alpha/2)=\chi^2_(24,0.025)=39.36`

`\chi^2_(n-1, 1-\alpha/2)=\chi^2_(24,0.025)=12.40`

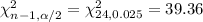
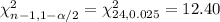
Then, the confidence interval for population variance is given by :-

`((24)( 51.3))/(39.36)\leq \sigma^2\leq((24)( 51.3))/(12.40)\\\\\approx31.28\leq\sigma^2\leq99.29`

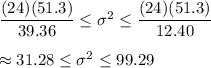
Hence, the 95% confidence interval for the population variance :

`31.28\leq\sigma^2\leq99.29`