Question

For sin2x+cosx=0, use a double-angle or half-angle formula to simplify the equation and then find all solutions of the equation in the interval [0,2π).

Answer 1

Explanation:

Given is a trignometric equation in x, as

`sin2x+cosx=0`

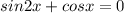
TO make it in one trig ratio, we can replace sin2x as 2sinx cosx

WE get now

`2sinxcosx+cosx=0\\`

`cosx(2sinx+1)=0\\cosx=0, sinx =-0.5\\`

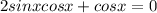
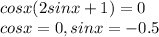
Principal solution is
`x=(\pi)/(2) , (-\pi)/(6)`

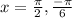
x = ±π/2 + 2kπ, where k is any integer or

x=±pi/6 +k pi, where k is any integer.

General solution is