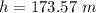Answer:
Explanation:
Let
h -----> the height of the building
x -----> the horizontal distance between the building and the tower
we know that
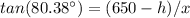
solve for x
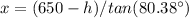 -----> equation A
-----> equation A

solve for x
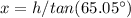 ------> equation B
------> equation B
equate equation A and equation B and solve for h


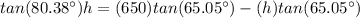
![h[tan(80.38\°)+tan(65.05\°)]=(650)tan(65.05\°)](https://img.qammunity.org/2020/formulas/mathematics/high-school/1esi5scd4lues3tudpmo3yagj5538iwhh6.png)
![h=(650)tan(65.05\°)/[tan(80.38\°)+tan(65.05\°)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/au1i1kea0qtrtads6yobmoiiboghxjf1dh.png)