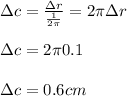Question

The measurenicnt of the circumference of a circle is found to be 56 centimeters. The possible error in measuring the circumferencc is 1.2 centimeters.

(a) Approximate the percent error in computing the area of the circle.
(b) Estimate the maximum allowable percent error in measuring the circumference if the error in computing the area cannot exceed 3%.

Answer 1

(a) Approximate the percent error in computing the area of the circle: 4.5%

(b) Estimate the maximum allowable percent error in measuring the circumference if the error in computing the area cannot exceed 3%: 0.6 cm

Explanation:

(a)

First we need to calculate the radius from the circumference:

`c=2\pi r\\r=(c)/(2\pi ) \\c=8.9 cm`

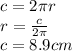
I leave only one decimal as we need to keep significative figures

Now we proceed to calculate the error for the radius:

`\Delta r=(dt)/(dc) \Delta c\\\\(dt)/(dc) =    (1)/(2 \pi ) \\\\\Delta r=(1)/(2 \pi ) (1.2)\\\\\Delta r= 0.2 cm`

`r = 8.9 \pm 0.2 cm`

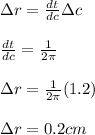
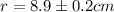
Again only one decimal because the significative figures

Now that we have the radius, we can calculate the area and the error:

`A=\pi r^(2)\\A=249 cm^(2)`

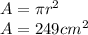
Then we calculate the error:

`\Delta A= ((dA)/(dr) ) \Delta r\\\\\Delta A= 2\pi r \Delta r\\\\\Delta A= 11.2 cm^(2)`

`A=249 \pm 11.2 cm^(2)`

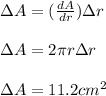
Now we proceed to calculate the percent error:

`\%e =(\Delta A)/(A) *100\\\\\%e =(11.2)/(249) *100\\\\\%e =4.5\%`

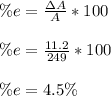
(b)

With the previous values and equations, now we set our error in 3%, so we just go back changing the values:

`\%e =(\Delta A)/(A) *100\\\\3\%=(\Delta A)/(249) *100\\\\\Delta A =7.5 cm^(2)`

Now we calculate the error for the radius:

`\Delta r= (\Delta A)/(2 \pi r)\\\\\Delta r= (7.5)/(2 \pi 8.9)\\\\\Delta r= 0.1 cm`

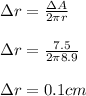
Now we proceed with the error for the circumference:

`\Delta c= (\Delta r)/((1)/(2\pi )) = 2\pi \Delta r\\\\\Delta c= 2\pi 0.1\\\\\Delta c= 0.6 cm`