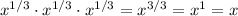Question

Please help
Show work
18 points!
Geometry - 5 questions
Thankyou❤️

Answer 1

1. No it is not equivalent

2. √x

3. ⁸√x

4.
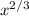`x^(2/3)` or ∛x²

5. B and D

Explanation:

1. It is not equivalent because of the rules of exponents:

`a^(m) \cdot a^(n) = a^(m+n)`

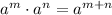
So if we take in your problem, you would have the following:

`x^3 \cdot x^3 \cdot x^3 = x^(3+3+3) = x^9`

while...

`x^(3.3.3) = x^(27)\\\\x^9\\eq x^(27)`

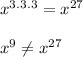
2. Following law of exponents again, when the exponent is negative you get the inverse, so if the exponent is negative the top goes to the bottom and the bottom goes to the top.

`\frac{1}{x^{(-3)/(6)}}=x^{(3)/(6)}=x^{(1)/(2)}=√(x)`

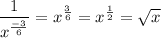
This can be changed into a radical, where the denominator will be the root, and the numerator will be the exponent the base is raised.

So...

`x^{(1)/(2)} = √(x)`

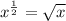
3. When multiplying radicals with like radicands remember the following:

`\sqrt[a]{a} \cdot \sqrt[b]{a} = \sqrt[a.b]{x}`

So let's take your problem:

`√(x)*\sqrt[4]{x} =\sqrt[2* 4]{x} = \sqrt[8]{x}`

4. Following law of exponents again, when dividing with the same bases but different exponents, you just copy the base and subtract the exponent of the denominator from the exponents of the numerator.

`(x^a)/(x^b) = x^(a-b)`

`\frac{x^{(5)/(6)}}{x^{(1)/(6)}} = x^{(5)/(6)-(1)/(6)} =x^{(4)/(6)}\\\\x^{(4)/(6)}=x^{(2)/(3)}=\sqrt[3]{x^2}`

5. Simplifying all terms:

A.
`\sqrt[4]{x^(3)} =x^{(3)/(4)}`

B.
`(1)/(x^(-1)) = x^(1) = x`

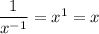
C. ¹⁰√x⁵·x⁴·x² = ¹⁰√x¹¹ = √x

D.
`x^(1/3)\cdot x^(1/3)\cdot x^(1/3) = x^(3/3) = x^(1) = x`