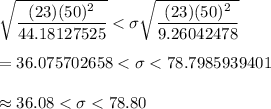Question

A factor in determining the usefulness of an examination as a measure of demonstrated ability is the amount of spread that occurs in the grades. If the spread or variation of examination scores is very small, it usually means that the examination was either too hard or too easy. However, if the variance of scores is moderately large, then there is a definite difference in scores between "better," "average," and "poorer" students. A group of attorneys in a Midwest state has been given the task of making up this year's bar examination for the state. The examination has 600 total possible points, and from the history of past examinations, it is known that a standard deviation of around 78 points is desirable. Of course, too large or too small a standard deviation is not good. The attorneys want to test their examination to see how good it is. A preliminary version of the examination (with slight modification to protect the integrity of the real examination) is given to a random sample of 24 newly graduated law students. Their scores give a sample standard deviation of 50 points. ​ Find a 99% confidence interval for the population standard deviation. a. 36.08 to 78.80 b. 57.49 to 125.57 c. 58.67 to 128.16 d. 56.28 to 122.93 e. 36.85 to 80.50

Answer 1

Answer: . a. 36.08 to 78.80

Explanation:

The confidence interval for population standard deviation is given by :-

`\sqrt{((n-1)s^2)/(\chi_(\alpha/2))}<\sigma\sqrt{((n-1)s^2)/(\chi_(1-\alpha/2))}`

Given : Sample size =
`n=24`

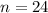
Significance level :
`\alpha:1-0.99=0.01`

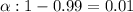
Using the chi-square distribution table , the critical values would be :-

`\chi_(n-1,\alpha/2)=\chi_(23, 0.005)=44.18127525`

`\chi_(n-1,1-\alpha/2)=\chi_(23, 0.995)=9.26042478`

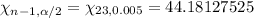
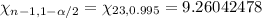
Then , a 99% confidence interval for the population standard deviation will be :-

`\sqrt{((23)(50)^2)/(44.18127525)}<\sigma\sqrt{((23)(50)^2)/(9.26042478)}\\\\=36.075702658<\sigma<78.7985939401\\\\\approx36.08<\sigma<78.80`