Question

if a cow costs 1$ a sheep costs 0.5$ and a horse cost 10$ and you have 100$ to buy 100 animals and you have to have one of each. how many of each did you buy?

Answer 1

5 cows of 5$, 90 sheep of 45$ and 5 horses of 50$.

Explanation:

Cost of 1 cow = $1

Cost of 1 sheep = $0,5

Cost of 1 horse = $10

Let number of cows be x and , number sheep be y and number of horses be z.

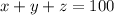`x+y+z=100`...(1)

`1\$x+0.5\$y+10\$z=100\$`

`10x+5y+100z=1000`

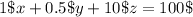
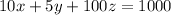
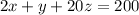`2x+y+20z=200`..(2)

Since , there should be minimum 1 animal. we will be using hit and trial method for the solution:

1) Put value of x =1 , in (1) and (2),we get two equation in two variables:

`y+z=99`

`y+20z=198`

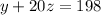
Solving above equation we get , y =93.79 , z= 5.21 (Not possible)

2) Put value of x = 2 , in (1) and (2),we get two equation in two variables:

`y+z=98`

`y+20z=196`

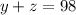
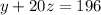
Solving above equation we get , y =92.85 , z= 5.15 (Not possible)

3) Put value of x = 5 , in (1) and (2), we get two equation in two variables:

`y+z=95`

`y+20z=190`

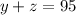
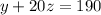
Solving above equation we get , y =90 , z= 5 (possible)

5 cows of 5$, 90 sheep of 45$ and 5 horses of 50$.