Question

39. | A car is traveling at a steady 80 km/h in a 50 km/h zone. A

police motorcycle takes off at the instant the car passes it, accel-
erating at a steady 8.0 m/s².
a. How much time elapses before the motorcycle is moving as
fast as the car?
b. How far is the motorcycle from the car when it reaches this
speed?

Answer 1

The time it takes for the motorcycle to be moving as fast as the car is approximately 2.775 seconds. The distance between the motorcycle and the car when the motorcycle reaches the same speed as the car is approximately 30.5 meters.

Step-by-step explanation:

a. To find the time it takes for the motorcycle to be moving as fast as the car, we need to compare their speeds. The car is traveling at a steady 80 km/h, which is equivalent to 22.2 m/s. The motorcycle is accelerating at 8.0 m/s². We can set up the equation v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time. Let's assume the motorcycle starts from rest, so its initial velocity is 0 m/s. Plugging in the values, we get 22.2 = 0 + (8.0)(t). Solving for t, we find t = 2.775 seconds.

b. To find the distance between the motorcycle and the car when the motorcycle reaches the same speed as the car, we can use the equation s = ut + 1/2at². Again, assuming the motorcycle starts from rest, its initial velocity is 0 m/s. Plugging in the values, we get s = (0)(2.775) + 1/2(8.0)(2.775)². Solving for s, we find s ≈ 30.5 meters.

Answer 2

a) 2.8 s b) 30.8 m

Step-by-step explanation:

a) For a uniform acceleration a the equation for velocity v is given by:

`v = at + v_0`

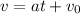
For the police car the given values are:

v₀ = 0, v = 80 km/h = 22.2 m/s , a = 8 m/s²

Solving for time t:

`t = (v - v_0)/(a) = 2.8 s`

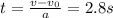
b) In this time t the distance x traveled by the car with uniform velocity v is given by:

`x = vt + x_o`

For the car the given values are:

v = 80 km/h = 22.2 m/s, x₀ = 0, t = 2.8 s

x = 61.7

The distance s traveled by the police car with uniform acceleration a is:

`s = (1)/(2) at^(2) + v_0t + x_0`

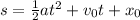
The given values are:

a = 8m/s², v₀ = 0, x₀ = 0, t = 2.8 s

s = 30.9 m

The difference between the distance x traveled by the car and the distance s traveled by the police is 30.8 m