Question

Point S is between R and T on line segment RT. Use the given information to write an equation in terms of x.

Solve the equation. Then find RS and ST.
a. RS = 2x-10. ST = x-4. and RT = 21
b. RS = 3x-16. ST = 4x-8. and RT= 60
c. RS= 2x-8. ST = 3x-10. and RT = 17​

Answer 1

Answer:
`\bold{a)\quad x=(35)/(3)\qquad RS=13(1)/(3)\qquad ST=7(2)/(3)}`

b) x = 12 RS = 20 ST = 40

c) x = 7 RS = 6 ST = 11

Explanation:

Use the Segment Addition Postulate: RS + ST = RT

a) (2x - 10) + (x - 4) = 21

3x - 14 = 21

3x = 35

x
`=(35)/(3)`

RS = 2x - 10

`=2\bigg((35)/(3)\bigg)-10`

`=(70)/(3)-(30)/(3)`

`=(40)/(3)`

`=\large\boxed{13(1)/(3)}`

ST = RT - RS

`=21-13(1)/(3)`

`=\large\boxed{7(2)/(3)}`

Use the same formula to solve for b and c

Answer 2

Given,

S is the between R and T on line segment RT.

Thus, RS + ST = RT,

RS and ST.

a. If RS = 2x-10. ST = x-4. and RT = 21,

2x - 10 + x - 4 = 21

3x - 14 = 21

3x = 35

`\implies x = (35)/(3)`

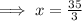
RS =
`2((35)/(3))-10=(70)/(3)-10=(40)/(3)`

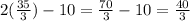
ST =
`(35)/(3)-4=(35-12)/(3)=(23)/(3)`

b. RS = 3x-16. ST = 4x-8. and RT= 60,

3x - 16 + 4x - 8 = 60

7x - 24 = 60

7x = 84

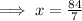`\implies x =(84)/(7)` = 12,

RS = 3(12) - 16 = 36 - 16 = 20,

ST = 4(12) - 16 = 48 - 16 = 32

c. RS= 2x-8. ST = 3x-10. and RT = 17​.

2x - 8 + 3x - 10 = 17

5x - 18 = 17

5x = 35

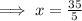`\implies x =(35)/(5)` = 7,

RS = 2(7) - 8 = 14 - 8 = 6,

ST = 3(7) - 10 = 21 - 10 = 11