Question

If the population of a particular country is growing at 3.2 % compounded​ continuously, how long will it take the population to triple​?

Answer 1

It will take 34.33

Explanation:

* Lets talk about the compound continuous growing

- Compound continuous growing can be calculated using the formula:

`A=Pe^(rt)`

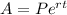
# A = the future value

# P = the initial amount

# r = the growing rate in decimal

# t = the time

* Lets solve the problem

- The population of a particular country is growing at 3.2 %

compounded​ continuously

∴ r = 3.2/100 = 0.032

- We need to find how long will it take the population to triple​

∵ The initial population is P

∴ A = 3P

∵
`A=Pe^(rt)`

∴
`3P=Pe^(0.032t)`

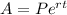
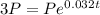
- Divide both sides by P

∴
`3=e^(0.032t)`

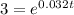
- Insert ㏑ for both sides

∴
`ln(3)=ln(e^(0.032t))`

- Remember
`ln(e^(n))=n`

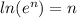
∴ ㏑(3) = 0.032t

- Divide both sides by 0.032

∴ t = ㏑(3)/0.032 = 34.33

* It will take 34.33