Question

erika says that no matter how many decimals places she divides to when she divides 1 by 3, the digit 3 in the quotient will just keep repeating. Is she correct? explain.

Answer 1

Yes she is correct because 1 divided by 3 will have an infinite number of 3s

Answer 2

Yes, Erica is correct.

We divide 1 by 3 as
`(1)/(3) =0.333333...`

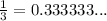
Now, the quotient is 0.333333...

Clearly, we can see that the 3 is repeating.

Now, the decimal expansion of any rational number is non-terminating repeating if the factors of the denominator is not of the form

`2^(m) *5^(n)` .

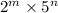Clearly, the factor of the denominator, i.e 3 is
`3*1`

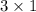
So, the factors are not of the form
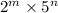`2^(m) *5^(n)` , the decimal expansion of
`(1)/(3)` is non-terminating repeating.

Hence, the digit 3 in the quotient is repeating.