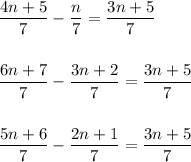Question

I have a question that I need answered quickly (it's late and my homework is due soon). I have a few algebra problems that say I need to write each fraction as a sum or difference. For example, 3n+5 over 7. Can someone explain how to solve this?

Answer 1

Answer:
`\bold{(3n)/(7)+(5)/(7)=(3n+5)/(7)}`

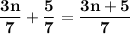
Explanation:

When adding (sum) or subtracting (difference) fractions, the denominator needs to be the same.

There are an infinite number of ways to create the numerator to result in 3n + 5 --> just make sure the denominator for each fraction is 7.

Examples of a sum:

`(3n)/(7)+(5)/(7)=(3n+5)/(7)\\\\\\(2n+5)/(7)+(n)/(7)=(3n+5)/(7)\\\\\\(2n+3)/(7)+(n+2)/(7)=(3n+5)/(7)`

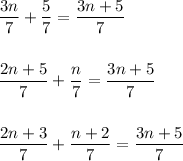
Examples of a difference:

`(4n+5)/(7)-(n)/(7)=(3n+5)/(7)\\\\\\(6n+7)/(7)-(3n+2)/(7)=(3n+5)/(7)\\\\\\(5n+6)/(7)-(2n+1)/(7)=(3n+5)/(7)`