Question

I need help on question 2 i need the simplified answer and the restrictions

Answer 1

x cannot be 5 or -3.

`(x+5)/(x+3)`

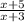
Explanation:

The restrictions for a fraction is that the bottom cannot be 0.

So if we find when the bottom is 0 we have found the values that x cannot be.

Let's solve x^2-2x-15=0.

Since the coefficient of x^2 is 1 all we have to do is find two numbers whose product is -15 and whose sum is -2.

Those numbers are -5 and 3 since (-5)(3)=-15 and (-5)+(3)=-2.

So the factored form of the equation is:

(x-5)(x+3)=0

This means either x-5=0 or x+3=0.

We do have to solve both.

x-5=0 can be solved by adding 5 on both sides.

x-5+5=0+5

x+0=0+5

x=5

x+3=0 can be solved by subtracting 3 on both sides.

x+3-3=0-3

x+0=0-3

x=-3

So x can be any number except x=5 or x=-3.

We already factored the bottom as (x-5)(x+3).

The top is a difference of squares, x^2-a^2,

which can be factored as (x-a)(x+a).

So the top factors as (x-5)(x+5).

The fraction can then be written as:

`(x^2-25)/(x^2-2x-15)=((x-5)(x+5))/((x-5)(x+3))`

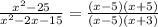
This can further simplified assuming x is not 5 we can write it as
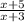`(x+5)/(x+3)`. I canceled the common factor of (x-5).