Answer:
The simplest form is tan(4x)
Explanation:
* Lets revise the identity of the compound angles
-
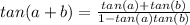
-
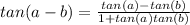
* Lets solve the problem
- Let 9x = 5x + 4x
∴ tan(9x) = tan(5x + 4x)
- Use the rule of the compound angle
∵
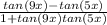 ⇒ (1)
⇒ (1)
∵
 ⇒ (2)
⇒ (2)
∵ tan(9x) = equation (2)
- Substitute (2) in (1)
∴
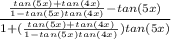
- Multiply up and down by (1 - tan(5x)tan(4x))
∴
![(tan(5x)+tan(4x)-tan(5x)[1-tan(5x)tan(4x)])/(1-tan(5x)tan(4x)+tan(5x)[tan(5x)+tan(4x)])](https://img.qammunity.org/2020/formulas/mathematics/middle-school/cqvghsj2qt0imdtypviav75gzldnlcbbv5.png)
- Simplify up and down
∴
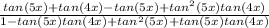
∴
![(tan(4x)+tan^(2)(5x)tan(4x))/([1+tan^(2)(5x)])](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8zz2m7txy9s7ele77qhcrf1fj5ijwepe3r.png)
- Take tan(4x) as a common factor up
∴
![(tan(4x)[1+tan^(2)(5x)])/([1+tan^(2)(5x)])](https://img.qammunity.org/2020/formulas/mathematics/middle-school/o59zp2actnpwsfaws9k4un9blg4jzsaldw.png)
- Cancel [1 + tan²(5x)] up and down
∴ The answer is tan(4x)