Answer:
0
Explanation:
We are given the following:
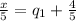 (equ. 1)
(equ. 1)
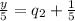 (equ. 2)
(equ. 2)
We are asked:
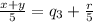 (equ. 3) , what is
(equ. 3) , what is
 ?
?
The
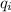 's represent the quotients you get.
's represent the quotients you get.
 is the remainder of dividing
is the remainder of dividing
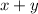 by 5.
by 5.
We know that
 is a number in {0,1,2,3,4}.
is a number in {0,1,2,3,4}.
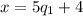 (I got this by multiplying both sides of equ 1. by 5.)
(I got this by multiplying both sides of equ 1. by 5.)
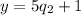 (I got this by multiplying both sides of equ 2. by 5.)
(I got this by multiplying both sides of equ 2. by 5.)
Let's add these equations together:
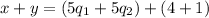
Factoring the 5 out for the
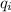 's part and simplify 4+1 gives:
's part and simplify 4+1 gives:
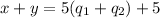
So
 can't be the remainder of dividing something by 5 but see that we can factor this right hand expression more as:
can't be the remainder of dividing something by 5 but see that we can factor this right hand expression more as:
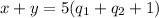
So
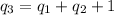 while there is no remainder (the remainder is 0).
while there is no remainder (the remainder is 0).
Let's do an example if you are not convinced at this point that the remainder will be 0.
So choose x=9 since 9/5 gives a remainder of 4.
And choose y=16 since 16/5 gives a remainder of 1.
x+y=9+16=25 and 25/5 gives a remainder of 0.