Answer:
Yes
Explanation:
If
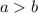 , then
, then
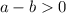 .
.
If
 are positive, then
are positive, then
 .
.
So if I multiply both sides of
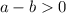 by
by
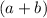 it will not effect the direction of the inequality since it is of positive value.
it will not effect the direction of the inequality since it is of positive value.
This actions gives us
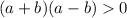 .
.
Using foil we can multiply the left hand side out resulting in:

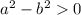
Add
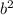 on both sides:
on both sides:
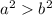 .
.
---------------------------------------------------------------------------
Also consider the function
 . This function increases after
. This function increases after
 is 0. This means as you increase the value for
is 0. This means as you increase the value for
 the value for
the value for
 increases for positive value inputs of
increases for positive value inputs of
 .
.