Question

Please help me thanks

Answer 1

d. is the closest one to fit.

Explanation:

At x=0 we see that y=1000 from the graph.

We are looking for an initial mass of 1000 from the equations.

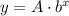`y=A\cdot b^(x)` tells us at
`x=0`,
`y=A`.

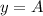If you are unsure that plug in 0 for
`x`:

`y=A \cdot b^0`

`y=A \cdot 1`

`y=A`

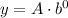
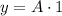
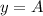
So we have here for this problem that
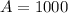`A=1000` since that is what happens at
`x=0`.

So far we know the equation is:

`y=1000 \cdot b^(x)`

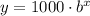
To find
`b` we need to look at another point on our graph.

At almost x=4, we see that y is about 500.

Let's plug this into our equation above:

`500=1000 \cdot b^(4)`

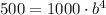
Divide both sides by 1000:

`(1)/(2)=b^4`

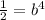
Take the fourth root of both sides:

`\sqrt[4]{(1)/(2)}=b`

So our equation is approximately:

`y=1000 \cdot (\sqrt[4]{(1)/(2)})^x`

The closet answer to this is d.

(a) isn't close because that would contain a negative factor which would include some kind of reflection through the x-axis.

(b) isn't close because again it includes a negative factor leading to some kind of reflection through the x-axis.

(c) isn't close because it's initial population is 1/2 and is increasing by factors of 1000.

(d) is the closest because it's initial population is 1000 and is decreasing because of the factors of ~1/2 .

Answer 2

D)

Explanation:

Based on the graph, you can determine that the function represents an exponential decay.

So by using the form f(x) = ab^x, an exponential decay function would mean that the decay factor (b) would be 0<b<1.

Additionally, the y-intercept of the function is 1000.

Thus the only answer the function can correspond to is answer D.

Reasons:

1) It has a growth factor of 1/2 which fits the requirements of the decay factor.

2) When 0 is inputted into the x value, a y value of 1000 is the result, which means that 1000 is the y-intercept.