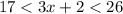Answer:
Part 1)
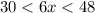
Part 2)
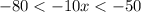
Part 3)
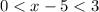
Part 4)
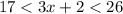
Explanation:
we know that
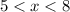
The solution for x is the interval ----> (5,8)
All real numbers greater than 5 and less than 8
Part 1) Find all possible values of the expression 6x
so
For x < 8
The expression value is 6x < (6)(8) -----> 6x < 48
For x > 5
The expression value is 6x > (6)(5) -----> 6x > 30
therefore
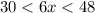
Part 2) Find all possible values of the expression -10x
so
For x < 8
The expression value is -10x > (-10)(8) -----> -10x > -80
For x > 5
The expression value is -10x < (-10)(5) -----> -10x < -50
therefore
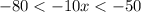
Part 3) Find all possible values of the expression x-5
so
For x < 8
The expression value is x-5 < 8-5 -----> x-5 < 3
For x > 5
The expression value is x-5 > 5-5 -----> x-5 > 0
therefore
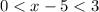
Part 4) Find all possible values of the expression 3x+2
so
For x < 8
The expression value is 3x+2 < 3(8)+2 -----> 3x+2 < 26
For x > 5
The expression value is 3x+2 > 3(5)+2 -----> 3x+2 > 17
therefore