Question

Solve for x in the equation

Answer 1

Fourth Option.
`x = (5)/(4) \pm (√(41))/(4)`

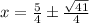
Explanation:

The given equation is:

`2x^(2)-5x+1=3`

In order to solve the equation, we need to make the Right hand side equal to Zero. Subtracting 3 from both sides, we get:

`2x^(2)-5x-2=0`

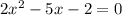
Since, this is a quadratic equation, we can use the quadratic formula to find the values of x which make the equation true. According to the quadratic formula values of x would be:

`x=\frac{-b \pm \sqrt{b^(2)-4ac} }{2a}`

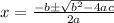
Here,

a = Coefficient of Squared term = 2

b = Coefficient of x = -5

c = Constant term = -2

Using these values in the formula, we get:

`x=\frac{-(-5) \pm \sqrt{(-5)^(2)-4(2)(-2)}}{2(2)}\\\\ x=(5 \pm √(25+16))/(4)\\\\ x=(5 \pm √(41))/(4)\\\\ x = (5)/(4) \pm (√(41))/(4)`

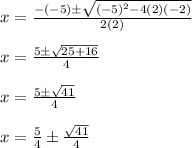
Hence, the Fourth Option gives the correct answer for x.