Answer:
a. (-1 , 1) is the point at 1 : 3 of the way from R to S
b. (5 , -3) is the point at 3 : 1 of the way from R to S
Explanation:
* Lets explain how to solve the problem
- If point (x , y) divide a line segment whose end points are
 and
and
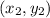 , at ratio
, at ratio
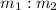 from the first point, then
from the first point, then
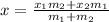 and
and
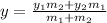
* Lets solve the problem
a.
∵ RS is a line segment whose end points are R (-4 , 3) and S (8 , -5)
∵ Point (-1 , 1) divides it at ratio
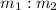 from R
from R
- By using the rule above
∴
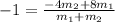
- By using cross multiplication
∴
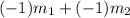 =
=
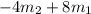
- By collecting
 in one side and
in one side and
 in the
in the
other side
∴
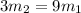
- Divide both sides by 3
∴
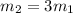
∴

∴ (-1 , 1) is the point at 1 : 3 of the way from R to S
b.
∵ RS is a line segment whose end points are R (-4 , 3) and S (8 , -5)
∵ Point (5 , -3) divides it at ratio
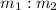 from R
from R
- By using the rule above
∴
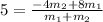
- By using cross multiplication
∴
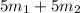 =
=
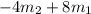
- By collecting
 in one side and
in one side and
 in the
in the
other side
∴
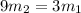
- Divide both sides by 3
∴

∴
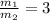
∴ (5 , -3) is the point at 3 : 1 of the way from R to S