Question

A truck using a rope to tow a 2230-kg car accelerates from rest to 13.0 m/s in a time of 15.0s. How strong must the rope be? μk = 0.373

Answer 1

The rope must have a force of 10084,21 N

Step-by-step explanation:

`ac=ac=(13)/(15) (m)/(s)`

`ac=ac=(13)/(15) (m)/(s)`

`ac = at = (13-0)/(15-0)`

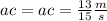
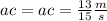
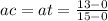
We replaced the known information in the equation(1):

vi = Initial speed = 0, ti = initial time = 0

Known information:

at: truck acceleration(m/s2)

ac: car acceleration
`(m)/(s^(2) )`

Kinematic analysis

The car acceleration is equal to the acceleration of the truck because the truck and the car are connected by the rope.

We apply Newton's first law to calculate the Normal force because there is no movement in the vertical direction:

`∑Fy= 0`

`N-W=0`

`N=W`

`N=21854 N`

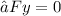
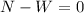
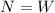
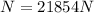
We replace the values of the mc and g in the equation(2):

`Wc= 2230*9.8`

`Wc=21854 N`

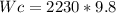
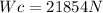
Normal force calculation:

Car weight calculation:

`Wc=mc*g`

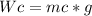
mc = Car mass = 2230kg

g = Gravity acceleration=9.8
`(m)/(s^(2) )`

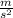
Friction force calculation (Ff):

We have the formula to calculate the friction force:

Ff = μk * N Equation (3)

μk: kinetic coefficient of friction

We know that μk = 0.373and N= 21854N , then we replaced this data in(3):

`Ff=0.373*21854`

`Ff=8151.54 N`

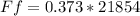
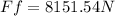
Calculation of the tension force in the ro pe (T):

We apply Newton's Second law to calculate the Normal force because there is no movement in the horizontal direction:

`∑Fx= mc*ac`

We take the sense of the forces like this:

positive to the right and negative to the left

`T-Ff=mc*ac`

`T=2230((13)/(15) + 8151.54`

`T=10084,21 N`

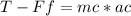
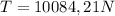
Answer: The rope must have a force of 10084,21 N