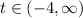Question

Solve 2 > -3t - 10
Please explain

Answer 1

`\large\boxed{t>-4\to t\in(-4,\ \infty)}`

Explanation:

We need to convert the inequality to the form t > some number

or t < some number.

`2>-3t-10\qquad\text{subtract 2 from both sides}\\\\2-2>-3t-10-2\\\\0>-3t-12\qquad\text{add}\ 3t\ \text{to both sides}\\\\0+3t>-3t+3t-12\\\\3t>-12\qquad\text{divide both sides by 3}\\\\(3t)/(3)>(-12)/(3)\\\\t>-4`

If you want to draw a solution on a numeric line.

for <,> - open circle (the number is not in the set of solutions)

for ≤, ≥ - closed circle (the number is in the set of solutions)

for <, ≤ - draw a line to the left

for>, ≥ - draw a line to the right.

We have t > -4

open circle, a line to the right (look at the picture).

If you want the solution in an interval, then

`t\in(-4, \infty)`

Answer 2

Hello there!

In this question, we're solving for t in the inequality.

Solve:

2 > -3t - 10

Add 10 to both sides

12 > -3t

Divide both sides by -3, also flipping the inequality since you're dividing by a negative

-4 < t

The t must be in the left side, so we would flip the whole equation.

t > -4

Answer: t > -4

I hope this helps!

Best regards,

MasterInvestor