Answer:
Both are not inverse functions.
Explanation:
To find : Determine whether each pair of functions are inverse functions ?
Solution :
To determine the functions has to satisfy the condition,
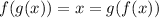
1)
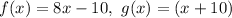
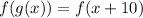
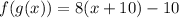
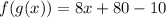

As

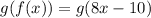
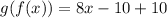
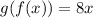
As the condition is not satisfied.
2)
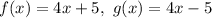
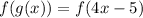
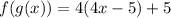
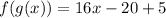
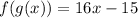
As

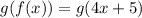
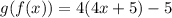
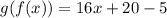

As the condition is not satisfied.
Both are not inverse functions.