Question

What is the area of rectangle ABCD in square units ?

Answer 1

Step-by-step explanation:

Square units = √( 4^2 + 1^2) * √( 8^2 + 2^2)

= √17 * √68

= √1156

= 34

Answer 2

34 square units

Step-by-step explanation:

In any rectangle, each two opposite sides are equal

This means that, in the given rectangle:

AB = CD and AD = BC

Area of the rectangle is the product of its dimensions (length and width)

This means that:

Area of ABCD = AB × BC

1- getting the side length:

To get the side length, we will use the distance formula:

`D = \sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

For AB, we have:

A = (-1,4) which means that x₁ = -1 and y₁ = 4

B = (3,3) which means that x₂ = 3 and y₂ = 3

Substitute in the equation:

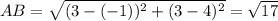`AB = √((3-(-1))^2+(3-4)^2) = √(17)` units

For BC, we have:

B = (3,3) which means that x₁ = 3 and y₁ = 3

C = (1,-5) which means that x₂ = 1 and y₂ = -5

Substitute in the equation:

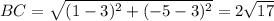`BC = √((1-3)^2+(-5-3)^2) = 2√(17)` units

2- getting the area:

Area of ABCD = AB × BC

Area of ABCD =
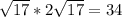`√(17) *  2√(17) = 34` square units

Hope this helps :)