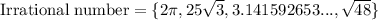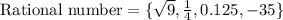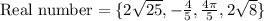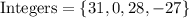Answer:
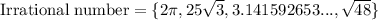
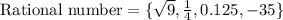
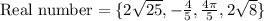
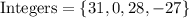
Explanation:
Set of Real numbers: The set of continuous quantity that can represent a distance along a line is known as set of all real numbers.
For example: -3.2, 4/5, π,√2, 4, etc.
Rational number: If a number can be defined in the form of p/q where, q≠0, then the number is called rational number.
For example: -3.2, 4/5, 2, etc.
Irrational number: If a number can't be defined in the form of p/q where, q≠0, then the number is called irrational number.
For example: π,√2, 3.6457..., etc.
Integers: A complete number that can be written without a fractional or decimal components, is called an integer.
For example: -2, 0, 5 etc.
Using the above definition we conclude that