Question

A spherically symmetric charged distribution has a charged density given by ρ = a / r, where a is a constant. Find the field within the sphere as a function of r. [

Answer 1

Electric field,
`E = (a)/(2epsilon)`

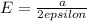
Given:

charge density,
`\rho = (a)/(r)`

a = constant

Solution:

Area of sphere =
`4\pi r_(2) dr`

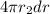
Small charge dq on a sphere of thickness r is:

dq =
`\rho * A* dr`

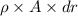
dq =
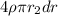`4\rho \pi r_(2) dr` (1)

Integrating both the sides, we get:

`dq = 4\rho \pi r_(2) dr`

`\int dq = \int (a)/(r)* 4\pi r^(2) dr`

`q(r)= 2\pi r^(2)a - 0 = 2\pi r^(2)a`

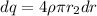
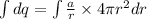
Therefore, the total charge enclosed by a sphere of radius r is
`q(r)= 2\pi r^(2)a`

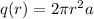
Now, by Gauss Law, flux emerging out of the surface is equal to
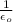`(1)/(\epsilon_(o))` times the total charge enclosed:

`A* E = (q)/(\epsilon_(o))`

`4\pi r^(2)* E = \frac{}{\epsilon_(o)}`

`E = (2\pi r^(2)a)/(\epsilon_(o))`

`E = (a)/(2epsilon)`

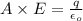
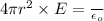
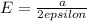
where

E = electric field