Question

A pressure of 3 atm was required to force water through an initially dry Teflon membrane of uniform pore size. Determine the pore size. (theta_water = 110 degree, gamma_water = 73mN/m)

Answer 1

Step-by-step explanation:

As it is given that
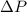`\Delta P` = 3 atm =
`3.04 * 10^(5) N/m^(2)`

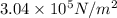
r = 73 mN/m

`\Theta` =
`110^(o)C`

As it is known that free energy of a wetting liquid in a solid-liquid interface is lower than the solid-gas interface free energy.

As a result, there will be spontaneous filling of pores but we need a non-reactive gas under the pressure so that the liquid can be forced out of the pores.

The pressure difference will be represented as
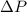`\Delta P`. Hence, work done by the gas to increase interface free energy is as follows.

`\Delta P = (rcos \Theta) ((dS)/(d\\u))`

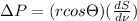
where,
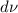`d\\u` = incremental volume of gas in the pore

dS = incremental solid-gas interface area due to
`d\\u`.

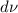So,
`((dS)/(d\\u))_(pore)` =
`((dS)/(d\\u))_(cylinder)`

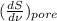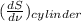
Therefore, formula to calculate pore size is as follows.

D =
`(4r cos \Theta)/(\Delta P)`

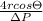
Putting the given values into the above formula as follows.

D =
`(4r cos \Theta)/(\Delta P)`

=
`(4 * 73 mN/m * cos(110^(o)))/(3.04 * 10^(5)N/m^(2))`

=
`0.33 m^(2)`

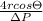
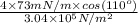
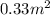
Thus, we can conclude that pore size is
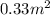`0.33 m^(2)`.