Answer:
The value of the inductance is 175.9 mH.
Step-by-step explanation:
Given that,
Capacitor
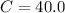
Frequency = 60.0 Hz
The inductor and capacitor is connected in parallel, the voltage across each of these elements is the same.
We have,
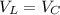
Using ohm's law
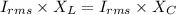
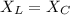
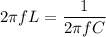
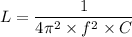
Put the value into the formula
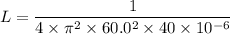
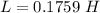
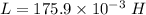
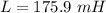
Hence, The value of the inductance is 175.9 mH.