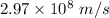Answer:
The velocity of rocket relative to ship is
Step-by-step explanation:
Given that,
Velocity of spaceship relative to earth
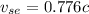
Velocity of rocket relative to earth
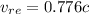
We need to calculate the velocity of rocket relative to ship
Using formula of relativistic velocity
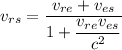
Put the value into the formula
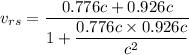
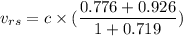
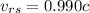

Hence, The velocity of rocket relative to ship is