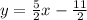Question

Through ( 3,2) parallel to y=5/2x-5 . What is the slope intercept form of the equation

Answer 1

y=(5/2)x+(-11/2)

Problem: What is the slope-intercept form for a line going through (3,2) and is parallel to y=(5/2)x-5?

Explanation:

Parallel lines have the same slope.

The slope-intercept form of a line is y=mx+b where m is the slope and b is the y-intercept. So we see that m=5/2 since that is the slope of y=5/2 x-5.

y=(5/2)x+b

We know (x,y)=(3,2) is a point on the line so replacing x with 3 and y with 2 gives:

2=(5/2)(3)+b

2=(15/2)+b

Subtract 15/2 on both sides:

2-(15/2)=b

Simplify:

(4-15)/2=b

(-11/2)=b

So the equation is:

y=(5/2)x+(-11/2)

Answer 2

`y=(5)/(2)x-(11)/(2)`

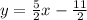
Explanation:

The equation of a line has the following form:

`y=mx+b`

Where m is the slope of the line and b is the intercept with the y axis.

If two lines of slopes m and n are parallel then it is true that:

`m=n`

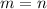
For the line
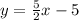`y =(5)/(2)x-5` the slope is:
`m=(5)/(2)`

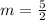
So the slope of the parallel line is:

`m=(5)/(2)`

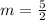
So the equation is:

`y=(5)/(2)x+b`

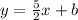
To find b we substitute the point (3, 2) in the equation and solve for b

`2=(5)/(2)(3)+b`

`b=2-(15)/(2)`

`b=-(11)/(2)`

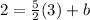
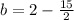
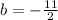
Then the equation of the line in the form of pending interception is:

`y=(5)/(2)x-(11)/(2)`