Step-by-step explanation:
The given data is as follows.
Volume of water = 0.25

Density of water = 1000
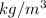
Therefore, mass of water = Density × Volume
=

= 250 kg
Initial Temperature of water (
 ) =
) =
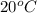
Final temperature of water =
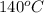
Heat of vaporization of water (
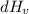 ) at
) at
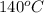 is 2133 kJ/kg
is 2133 kJ/kg
Specific heat capacity of water = 4.184 kJ/kg/K
As 25% of water got evaporated at its boiling point (
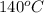 ) in 60 min.
) in 60 min.
Therefore, amount of water evaporated = 0.25 × 250 (kg) = 62.5 kg
Heat required to evaporate = Amount of water evapotaed × Heat of vaporization
= 62.5 (kg) × 2133 (kJ/kg)
=
 kJ
kJ
All this heat was supplied in 60 min = 60(min) × 60(sec/min) = 3600 sec
Therefore, heat supplied per unit time = Heat required/time =
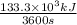 = 37 kJ/s or kW
= 37 kJ/s or kW
The power rating of electric heating element is 37 kW.
Hence, heat required to raise the temperature from
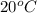 to
to
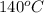 of 250 kg of water = Mass of water × specific heat capacity × (140 - 20)
of 250 kg of water = Mass of water × specific heat capacity × (140 - 20)
= 250 (kg) × 40184 (kJ/kg/K) × (140 - 20) (K)
= 125520 kJ
Time required = Heat required / Power rating
=
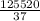
= 3392 sec
Time required to raise the temperature from
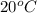 to
to
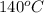 of 0.25
of 0.25
 water is calculated as follows.
water is calculated as follows.
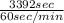
= 56 min
Thus, we can conclude that the time required to raise the temperature is 56 min.