Answer:1) 100 gm mass should be placed at 95 cm mark.
2) Mass of 112.5 gm should be placed at 90 cm mark.
Step-by-step explanation:
For equilibrium of the meter stick the sum of the moment's generated by the masses should be equal and opposite
Answer to part b)
Since a meter stick is 100 cm long and it is pivoted at it's center i.e at 50 cm
Thus
1) Moment generated by 100 gm mass about center =
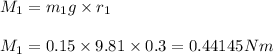
Let a mass 'm' be placed at 90 cm mark thus moment it generates equals
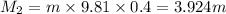
Equating both the moments we get
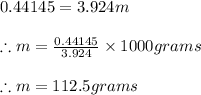
Answer to part a)
Let the 100 grams weight be placed at a distance 'x' right of center
Moment generated by 100 grams weight equals
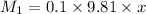
equating the moments of the forces we get

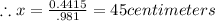
thus the mass of 100 gm should be placed at 95 cm mark in the scale.