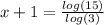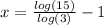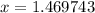Answer: Third Option
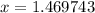
Explanation:
We have the following exponential equation
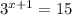
We must solve the equation for the variable x
To clear the variable x apply the
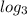 function on both sides of the equation
function on both sides of the equation
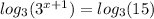
Simplifying we get the following:

To simplify the expression
 we apply the base change property
we apply the base change property
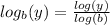
This means that:
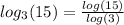
Then: