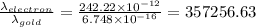Question

Compare the wavelength of a low-energy electron (???? = 0.01 c) to that of a gold atom. Use the De Broglie relation.

Answer 1

The wavelength of electron is 357256.63 times more than that of gold atom travelling at same speed.

Step-by-step explanation:

The de-broglie wavelength is obtained using the formula

`\lambda =(h)/(mv)`

For an electron we have

`m=9.11* 10^(-31)kg`

`v=0.01c=0.01* 3* 10^(8)m/s=3* 10^(6)m/s`

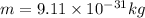
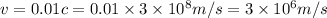
Using these values in the relation we get

`\lambda _{electron)=(6.62* 10^(-34))/(9.11* 10^(-31)* 3* 10^(6))`

`\therefore \lambda _(electron)=242.22* 10^(-12)m`

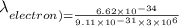
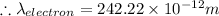
For a gold atom we have

`m=3.27* 10^(-25)kg`

`v=0.01c=0.01* 3* 10^(8)m/s=3* 10^(6)m/s`

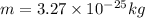
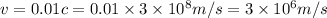
Using these values in the relation we get

`\lambda _{gold)=(6.62* 10^(-34))/(3.27* 10^(-25)* 3* 10^(6))`

`\therefore \lambda _(gold)=6.748* 10^(-16)m`

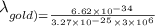
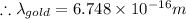
thus we can write

`(\lambda _(electron))/(\lambda _(gold))=(242.22* 10^(-12))/(6.748* 10^(-16))=357256.63`